Back to Table of Contents

40917-B6
Research in Statistical Physics of DNA Unzipping and Epitaxial Growth

Puiman Lam, Southern University

  Statistical Mechanics of a Chain in a Vertical Vibrating Tube

���� The compaction behavior of a granular material inside a vertical vibrating tube under gravity has been very well studied. Here we study the case when� the granular material is replaced by a long chain of monomers, each of mass m. For convenience we take the cross-section of the tube to be a square of size d x d,� under a gravitation field g. The tube with the chain is shaken by a sinusoidal vibration with angular frequency w and amplitude A. We study this model using a self-avoiding walk model. We find that fluctuation in the height of the chain obey a scaling behavior such that the fluctuation is proportional to the length of the chain. In addition, the distribution in the height of the chain obeys the Fermi distribution.

���� We can define an effective temperature T (with unit of energy) such that the kinetic energy per monomer due to shaking is equal to T (Boltzman� constant taken to be 1) :

������������������������������������������� .

In terms of G=Aw²/g, this can be written as T=mAGg/2.

���� We have simulated the system using a self-avoiding walk on a simple cubic lattice, with lattice constant a. A particular configuration of the chain is characterized by its total potential energy given by U(K)=Kamg.� K is an integer given by

�������������������������������� K=k₁+ k₂+ k₃+ k₄+�+ k_N

where the integers k_i give heights (in units of a) of the i-th monomer. The average height h of the monomers in this configuration is then given by h=Ka/N.

���� The canonical partition function of the chain is given by

��������������� ,

where the sum is over all configurations of the chain.

���� In terms of a dimensionless temperature T^*=AG/(2a), the partition sum can be written as

�����������������

The average height of the polymer over all possible configurations is given by

����������� .

The fluctuation in the average height is given by

����������

����

The fluctuation (Dh)² versus T^* obey a scaling relation. Such a scaling plot is shown in Figure 1, where we have plotted (Dh)²/N versus T^*/N. In Figure 2 we show the probability distribution P(h) as a function of h, for different temperatures T^*=2,4,6,8 and �, for a chain with N=60 monomers, in a tube of width d=3, on the square lattice. From Figure 2 and from similar figures for larger N we can see that the distribution becomes a Fermi distribution for large N.

������������������������ ����������������������

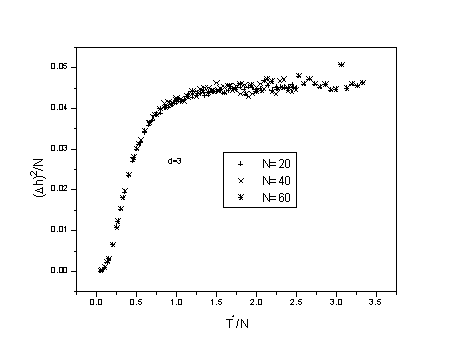
���������������������������������������������������� Figure 1

��������������� ����������

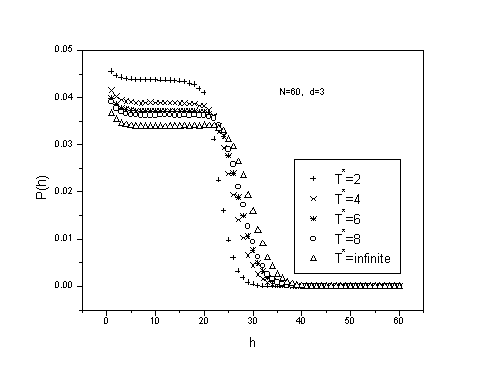
������������������������������������������������������������������� Figure 2����������������������

Back to top