Back to Table of Contents

44850-AC6
Simulation of Photochemical Processes and Their Nonlinear Optical Signature via the Generalized Quantum Master Equation

Eitan Geva, University of Michigan

The funding over the first year of this grant was used for partially supporting research projects performed by two graduate students and one postdoctoral fellow. The research projects involved using the Nakajima-Zwanzig generalized quantum master equation for describing photochemical processes in the condensed phase. This equation provides a general, and formally exact, prescription for simulating the dynamics of a quantum system coupled to a quantum bath. In this equation, the memory kernel accounts for the influence of the bath on the system's dynamics, and the inhomogeneous term accounts for initial system-bath correlations. We developed a new method for calculating the memory kernel and inhomogeneous term for arbitrary initial state and system-bath coupling. The new approach represents a significant improvement over a previously proposed scheme in the following respects:

• The new approach can accommodate a wide range of possible projection operators, while the previously proposed scheme was derived for a specific choice.

• Within the new approach, the memory kernel is obtained by solving a single Volterra equation, instead of the two coupled Volterra equations required by the previous approach.

• The new approach includes a new scheme for computing the inhomogeneous term.

• The new approach is applicable to driven systems with explicitly time-dependent Hamiltonians.

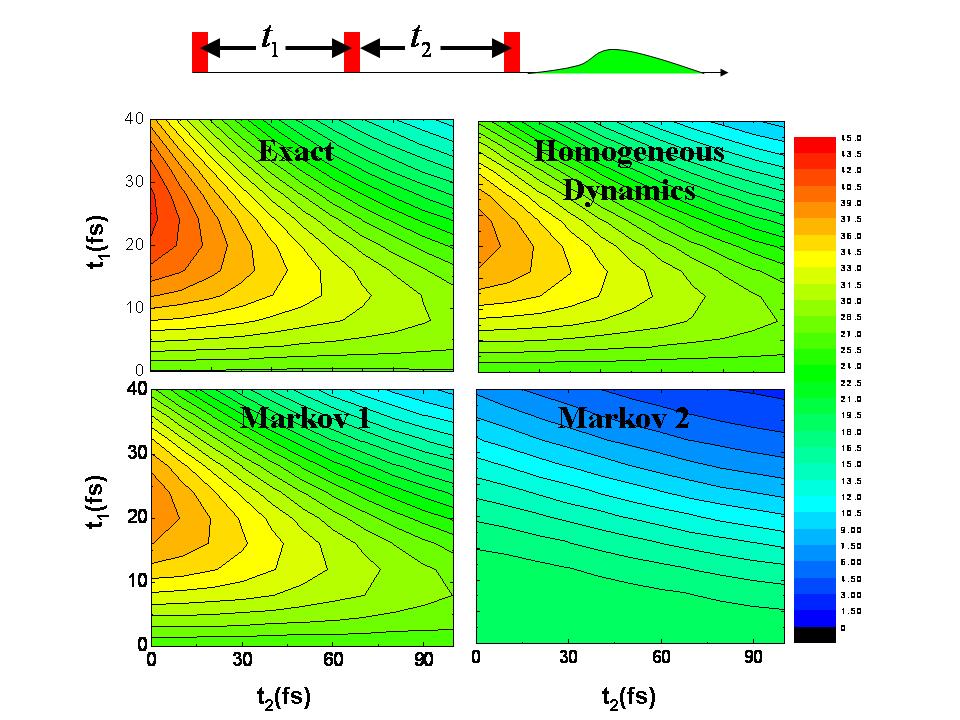
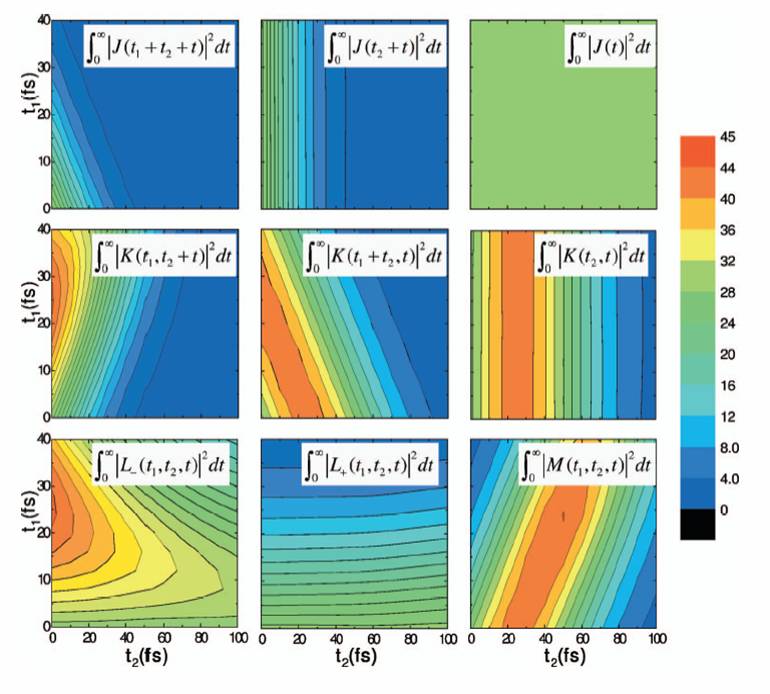
Figure 1: Homodyne-detected integrated three-pulse photon echo as function of times intervals between the pulses, in the case of a two-state chromophore in an atomic liquid. Shown are the exact results as well as results obtained based on assuming homogeneous dynamics and Markovity. For more details, see Ka et al J. Chem. Phys. 125 124509 (2006). 

In a follow-up study, we formulated the electronic dephasing dynamics of a solvated chromophore in terms of a generalized quantum master equation. Within this formulation, one describes the effect of the nuclear degrees of freedom on the electronic degrees of freedom in terms of a memory kernel function, which is explicitly dependent on the initial solvent configuration. This led to a new and rigorous way for defining “homogeneous dynamics” as the limit in which the memory kernel becomes independent of the initial configuration. The new method also provided a convenient framework for exploring the Markovity of the dephasing process by comparing the results obtained via the non-Markovian master equation to these obtained via its Markovian counterpart. The homogeneous memory kernel was calculated for a two-state chromophore in liquid solution, and used to explore the sensitivity of photon echo signals to the heterogeneity and non-Markovity of the underlying solvation dynamics (see Fig. 1).

We have also calculated nonlinear spectroscopic signals in liquid solution without treating the field-matter interaction in a perturbative manner. The calculated overall electronic polarization was resolved into its directional components via the method of Seidner et al. [J. Chem. Phys. 103, 3998 (1995)]. It was shown that the time dependence of the directional components is independent of laser intensity in the impulsive pulse regime, which allowed for flexibility in choosing the procedure for calculating optical response functions. The utility and robustness of the nonperturbative procedure was demonstrated in the case of a two-state chromophore solvated in a monoatomic liquid, by calculating nonlinear time-domain signals in the strong-field, weak-field, impulsive, and nonimpulsive regimes (see Fig. 2).

Figure  SEQ Figure \* ARABIC 2: The nine homodyne-detected integrated optical response functions as obtained from the overall polarization via the nonperturbative method. For more details, see Ka et al J. Chem. Phys. 125 214501 (2006).  

Back to top