In the second year of the project, we have refined the analytical model of the flow inside fully submerged thermocapillary-driven droplets by computing corrections to the interior and exterior flows arising due to interaction with the free surface of the liquid substrate. We have developed a computational procedure that generates a series of corrections to an unbounded flow by subsequently reflecting the exterior flow field about the plane interface of the substrate fluid and the spherical surface of the droplet, which insures that the proper boundary conditions at both interfaces are satisfied to a given order in the small parameter (the ratio of the droplet radius to the distance to the substrate surface). We have thus computed the interior and exterior flows in explicit analytical form.

In a parallel investigation, a numerical model of a thermocapillary-driven droplet suspended at the interface of the liquid substrate was constructed. Despite the somewhat different geometry (unlike the numerical model, the analytical one assumes the droplet is completely submerged), the two models produce interior flows that are in qualitative agreement for the case of a horizontal imposed temperature gradient. In the experiment, the temperature gradient is likely to have a significant vertical component. Therefore, the experimental setup has been redesigned to perform the measurements of both the temperature gradients driving the flow and the flow field inside the droplet. Once the experimental measurements are completed, the predictions of the numerical model (with boundary conditions matching the experiment) will be compared with experimentally measured flow field and the predictions of the analytical model, with the latter adjusted, if necessary.

In a separate study, mixing properties of time-periodic flows were investigated using a model of a Lorenz force-driven cellular channel flow with rectangular geometry. The mixing mechanism was found to have much in common with the case of thermocapillary-driven droplets. Again, the adiabatic invariant (AI) which emerges in the absence of time-periodic modulation of the flow was found to be destroyed by the modulation for streamlines crossing certain (resonance) surfaces. However, there are two significant differences with the steady flows. First of all, for the time-periodic flow, the frequency of the steady component of the flow does not vanish on these surfaces, but rather is in resonance with the non-zero modulation frequency of the time-periodic component. Second, there are multiple resonance surfaces (where the two frequencies are in a ratio of m:n with m and n integer).

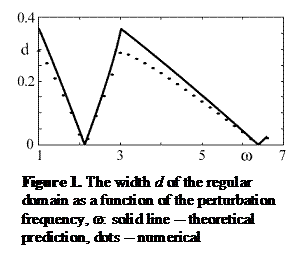We have determined that at resonance crossings two qualitatively different phenomena – scattering on resonance and capture into resonance – can occur, while only the former contributes significantly to the change in the AI. Just like in the case of a steady flow, the physical space was found to be split between the regular domain (composed of trajectories that do not cross any resonance surfaces), where mixing is absent, and the chaotic domain (composed of trajectories that cross a resonance and hence undergo a change in the value of the AI), where mixing takes place.

We have computed the magnitude of the jump of the AI on crossing a resonance surface and discovered that resonances with m > 1 or n-even do not lead to changes in the AI. The jump magnitude was found to decrease both with the magnitude of the time-dependent component of the flow (as its square root) and with the order n of the resonance. The dependence on n was found to be exponential, so the resonances are strongly ranked by their importance, with 1:1 resonance being the strongest (most efficient in mixing). We discovered the global mixing properties of the flow to exhibit a pronounced resonant dependence on the modulation frequency and have shown that, by choosing the modulation frequency appropriately, essentially complete mixing can be achieved.

The funding provided under this grant had a big impact on the PI's career by allowing him to build a group of students and postdocs working on different aspects of mixing at the microscale. The funding has also benefited the professional development of students (a graduate and two undergraduate) and (two) postdocs associated with the research project. The project formed the foundation for a thesis that is about to be completed by a graduate student and will result in two publications (to be submitted shortly). An undergraduate student took full advantage of the research opportunities offered by the project, learning many new numerical and analytical techniques. He is a co-author of two papers produced by our group (one published in Physical Review Letters, another to be submitted shortly) and a recipient of several awards for outstanding undergraduate research.