AmericanChemicalSociety.com

Introduction:

Suspension currents are ubiquitous in nature. They include avalanches, sand storms and deep-sea sediment slides. They self-sustain by maintaining a density difference with the surrounding ambient fluid by eroding and suspending particles from the ground. We investigate them with experiments, theory and numerical simulations. Our analysis of these flows is aimed at establishing how the characteristic shape of the current's head changes as a function of density difference, which in itself depends upon the basal erosion rate.

Experimental Setup:

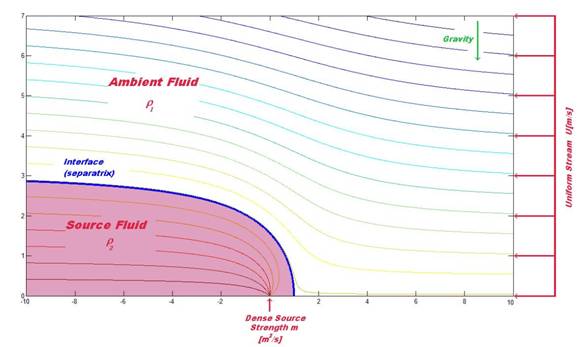
Figure 1: Rankine half body schematic diagram. Uniform velocity U [m/s], source strength m [m^2/s] (volume flowrate per unit width).

We have built a water flume experiment with uniform stream and isotropic source flow. To reach high Reynolds numbers while minimizing parasitic eddies in the main flow, we have installed a honeycomb mesh section that reduces upstream turbulence.  Our experiments inject a dense solution containing a fluorescent tracer to identify its motion. The dense fluid injection is isotropic and distributes uniformly both radially and longitudinally. To ensure uniformity of the source flow, we are installing a valve system containing small tubes to feed into the injection nozzle.

Maintaining the source fluid injection as two dimensional is a critical part of the experimental procedure. To that end, we installed a new pump driving the source fluid at its optimum flow rate, such that the main flume flow rate is independent from potential head changes that can cause oscillations, thus maintaining the position of the dense front at a stable location. We also created a model of the flume that predicts pressure losses in the flow in terms of flow rate.

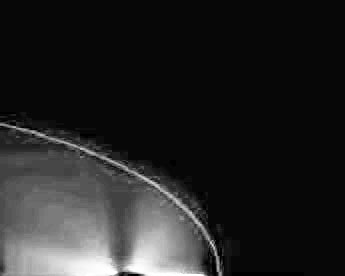
Figure 2: Time-averaged composite of 500 photographs of the Rankine half body in experiments with superimposed theoretical solution. Conditions are U=15 cm/s and m=0.047 m^2/s, for water and fluorescein.

We further improved our image acquisition system with a parabolic mirror and high-power light source. These ensure that a light sheet of constant cross section is achieved during each experiment. Camera positioning has also been optimized to produce images with repeatable concentration scale from flume data.

Theory:

We have developed a theory based upon the polar coordinate solution to the Laplace equation. In inviscid flow theory, the Rankine half body is created by inserting an isotropic source into a uniform stream. We perturb the streamfunction by introducing a small density variation between the ambient and source fluid. This causes small variations in both the shape of the interface between the fluids and the velocity and pressure on either side of this interface.

The front is located at the zeroth streamline. Taking the source fluid alone, we can determine the equation for the non dimensional interface location R_sep based upon the non-dimensional streamfunction Psi(Eq1),

Eqn 1  

Eqn 2

where r is the radial dimension, theta is the angle in polar coordinates, m is a measure of the non-dimensional source strength and B₁ is a coefficient calculated by our solution scheme.

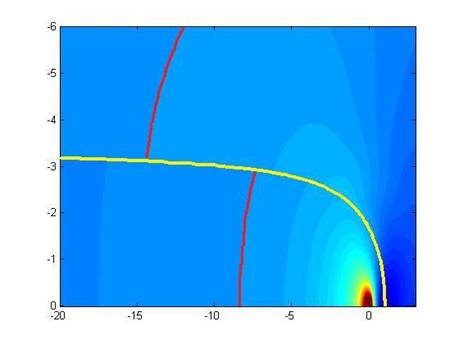
Our analysis reveals a discontinuous velocity profile at the fluid interface, pointing towards Kelvin-Helmholtz instabilities. Figure 3 illustrates the jump in fluid velocity that occurs across the interface for a given density difference.

Figure 3: Dimensionless velocity field for the density perturbed Rankine half body interface outlined in yellow. Note the shear layer at the interface illustrated by the red velocity contour.

Simulations

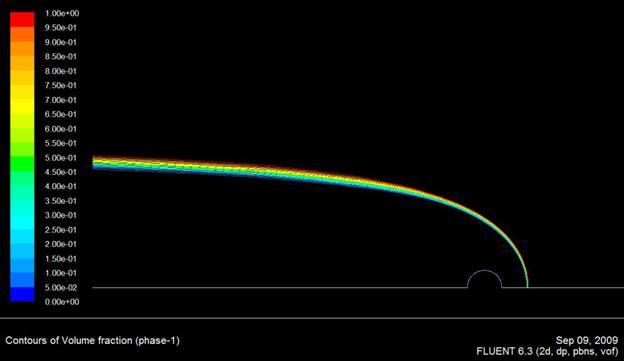
We employ ANSYS Fluent commercial CFD software to create a model of the Rankine half body. The simulation reproduces the analytically-derived position of the interface and the velocity field.

We pinpoint the location of the separatrix by initializing the source and ambient fluids as two separate immiscible flows. This multiphase model uses an interface tracking method to determine the front location as a function of time until the final steady state solution is produced. A density change can be created by changing the properties of either distinct fluid phases. Preliminary results of density difference analysis from this simulation indicate good agreement with the theory at low density differences. 

Figure 4: Rankine half body produced by simulating two immiscible fluids from the main stream and source. The interface between ambient and source fluid is shown as a narrow peak in the 2D contours of phi(1-phi), where phi is the volume fraction of one of the fluids.

Future Work:

We are designing and installing a new control valve system for the dense fluid injection. This will increase the uniformity of our flow rates from the source. We will also introduce a basal slope angle to the flume and create density differences in these experiments. We are presently carrying out simulations to examine both the effects of a combined slope and density difference. We will also adapt the boundary conditions of the simulation to model viscous floor effects. Introducing the effects of viscosity and turbulent closures into the model will give us greater insight into experimental observations.