AmericanChemicalSociety.com

This project aims to develop and apply molecular simulation methods that can aid in the prediction of crystalline polymorphs. Prediction of stable crystalline polymorphs should be completed by examining the relative free energies of candidate structures. In practice this is almost always done by examining the lattice energy alone, ignoring entropic contributions to the free energy. The error incurred with this procedure is generally considered to be of the order of the difference between candidate structures, but nevertheless the practice persists because it is inconvenient to consider the entropy rigorously, and approximate methods that introduce entropy tend not to lead to greater success in predicting the observed polymorphs. Such applications leave open the question as to whether failure of the prediction is due to inadequacies of the molecular model, or due to the approximations introduced to estimate the free energy. A major goal of this work is to establish the significance of the entropy (and its neglect) as a source of error in polymorph prediction efforts.

Rigorous methods to compute the free energy are seldom applied because they are tedious and computationally intensive. Thus a key component of this work is the development and/or improvement of such methods. To this end we are considering techniques that can yield an accurate free energy with minimum computational effort. Given that molecular simulation is required to render a good free-energy value, we aim to develop methods that require as few simulations as possible. Ideally one simulation would suffice, but experience with free-energy techniques tells us that at least two are needed to get an accurate and reliable result.  Accordingly, the approach we are pursuing is based on a system of coupled harmonic oscillators (which if taken by itself provides a well-studied means to estimate the free energy) combined with two-stage free-energy perturbation. Appropriate two-stage methods include umbrella sampling and overlap sampling, and our studies to date have looked at the ability of these to provide accurate free energies. Umbrella sampling requires just one simulation, but its proper application requires iteration on the umbrella potential; overlap sampling requires simulation of the harmonic reference and the target, but it does not require iteration for its application.

The key limitation in many cases can be cast in terms of the number of molecular degrees of freedom available to the system – larger systems with more degrees of freedom are more difficult to handle.  The difficulty is not just in the obvious added effort of simulating a larger system, which if programmed well can scale proportionally with the number of atoms; more important is the exponential increase in sampling needed to compute the free energy accurately. Thus in examining these methods we first focus on simple molecular models for which we can establish very accurate free energies via less efficient means such as thermodynamic integration, and with this baseline we can examine more efficient multistage perturbation methods. To this end we have first studied application to a system of monatomic soft spheres, with an inverse-12 repulsive potential. This model has a simple relation between its temperature and density dependence, so its thermodynamic state space is simple and consequently it provides a suitable starting point for the study of the efficacy of methods for different system sizes.

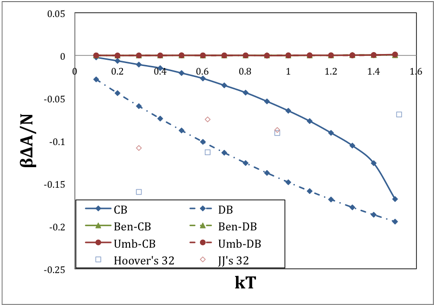
We examine two types of harmonic reference, one defined in terms of the derivative of the potential (indicated DB), and the other defined in terms of second-order correlations in atomic positions (indicated CB). For each, we examine both umbrella sampling (designated Umb) and overlap sampling (designated Ben, because it is known as Bennett's method when used in its optimized formulation). Typical results are shown in the following figure, which is for a system of 32 spheres.

FIG. 1. Error in free energy as a function of temperature, using various approximation methods. System size is 32 particles.

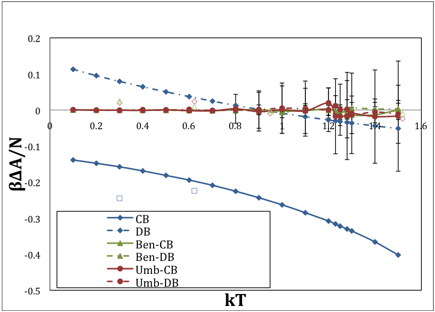
The ordinate shows the difference in the calculated free energy relative to that established by thermodynamic integration, so the zero line indicates exact correspondence. The blue lines are the uncorrected harmonic reference systems, and the red and green lines (which are mostly obscuring each other on the zero line) are the corrected forms. The result shows that for this system size, very good results can be obtained. In comparison, the following figure shows the corresponding results for 108 particles.  Although the data become quite noisy as melting is approached, it does still yield accurate results, but it seems to be reaching the limits of its capabilities.  We find that the Bennett's method implementation of overlap sampling with a correlation-based harmonic reference is the best choice among all considered.

FIG. 2. Same as Fig 1 but for 108 particles.

Knowing that we can get reliable results for sufficiently small systems, we can now go on to devise strategies to minimize finite-size effects.  This is a problem of a different nature. We can for example consider long-wavelength contributions to the free energy in a harmonic approximation, and couple them with the more rigorous short-wavelength results given by molecular simulation. Such an approach adds little to the computational burden, but has the potential to yield results that are accurate for systems much larger than is feasible by free-energy perturbation.  This investigation is currently underway. Once complete, we can take the guidelines developed from these simple-model studies and extend them in application to more complex models, including molecular crystals, which are of greater practical interest.