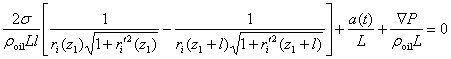AmericanChemicalSociety.com

The third year of the project has been principally devoted to building detailed theoretical understanding of how mechanical vibrations mobilize residual oil entrapped in porous space of oil reservoirs. Achieving such understanding is required before vibrational oil recovery can become a successful field technology. We have completed and validated a theoretical model that allows quantitative simulation of the dynamics of an oil droplet moving through a pore channel under the effect of all principal forces acting on oil. In a reservoir, background pressure gradient is the external forcing moving patches of oil to production wells. Entrapment of oil occurs when an isolated oil ganglion enters a constricted opening in a pore: capillary force resists the ganglion's motion through the narrow constriction. Vibrations provide an externally induced inertial forcing that can push the stuck blob over its “capillary barrier”, unplugging the flow. The motion is always resisted by viscous force. Our theory accounts for the four principal forces that govern the motion of the blob.

The model considers a body of non-wetting fluid (oil) flowing in an axisymmetric, sinusoidally constricted channel with a wetting film of constant thickness dh deposited on the channel's wall. The axial coordinate is z, the channel's wavelength is 2L, the blob's length is l, and the radius of the oil/water interface follows the sinusoidal shape r_i(z). The ganglion is pushed forward by a constant background pressure gradient  in the presence of externally induced vibrations producing a time-dependent acceleration of the pore's wall a(t).

The viscous friction affecting the ganglion's motion is introduced through the model of a Poiseuillean core-annular flow, in which oil is the core fluid and water is a wetting annulus adsorbed on the wall. The equation of motion of the ganglion is obtained as a balance of all body forces acting on oil:

.                         (1)

Here z₁/L is the ganglion's axial position,  is the average (constant) radius of the oil/water interface,  is the density of oil, σ is the oil/water interfacial tension, and μ_oil and μ_w are the viscosities of oil and water.  The “prime” symbol at r_i indicates the derivative with respect to z.

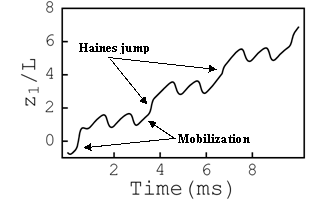
The solutions of equation 1 provide a complete time history of the blob's displacement. Figure 1 presents an example of the blob's motion, starting at the entrapped configuration when vibrations with the frequency of 1000 Hz have been turned on at t = 0 s. The sinusoidal pore has the maximum radius of 2×10^-5 m, the minimum radius of 10^-5 m; the film thickness is dh = 0.05× r_min, and  = 3.66×10⁷ N/m³. The oil becomes liberated in a fraction of the vibration period, is pushed over the capillary barrier, when the retarding effect of the capillary forces suddenly vanishes; the blob jumps out of the constriction and experiences a “Haines jump”.  The blob then reaches the next constriction, experiences two back-and-forth movements under the effect of the vibratory forcing, corresponding to two periods, becomes mobilized during the third period, experiences the next Haines jump, and then the pattern is repeated again.

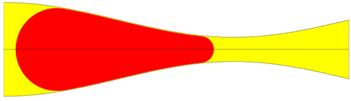
To mobilize an entrapped ganglion with given geometry at a given frequency of vibrations, a certain acceleration amplitude must be developed, which is called the threshold (or mobilization) amplitude. For practical purposes, it is important to verify if equation 1 provides an accurate prediction of the mobilizing frequency and amplitude. We validated such theoretical predictions against the computational-fluid-dynamics (CFD) code FLUENT, which solves the full system of equations of fluid mechanics for a two-phase flow on a spatial grid. An example of an initial geometry of a ganglion entrapped in a pore constriction, used as the starting configuration in FLUENT, is shown in Figure 2. Validations of the theory against FLUENT have been performed in the frequency range of 50-1000 Hz for the sinusoidal pores with the same minimum radius of 10^-5 m and the maximum radii of 2×10^-5 m and 4×10^-5 m, different film thicknesses dh, and the values of L = 10^-4 m and l = 0.6×L. Comparison of the solutions between CFD and equation 1 has shown that the simple dynamic model predicts the acceleration required to mobilize a static ganglion with the error of about 30 % or smaller, relative to CFD. This should be considered a practically satisfactory accuracy, considering the simplicity of the model and the ease of obtaining its numerical solutions. The advantage of using equation 1 can be illustrated as follows. Obtaining an estimate of the mobilizing amplitude of vibrations at a frequency of 50 Hz using CFD requires about three months of CPU time. On the other hand, such an estimate is obtained from the model equation in several seconds.

Figure 1. Axial position of the ganglion under the effect of vibrations calculated from equation 1.

Figure 2.  Initial geometry for the simulations in FLUENT.