AmericanChemicalSociety.com

This research program examines the mechanisms by which surfactants adsorb from an aqueous solution containing micellar aggregates onto an initially clean air/water interface. We focus our attention on spheroidal aggregates, and the nonionic poly(ethylene oxide) surfactant, C₁₄E₆, CH₃(CH₂)₁₃(OCH₂CH₂)₆OH, which forms spheroidal aggregates at room temperature above a critical concentration (the critical micelle concentration or CMC). When a fresh interface is created in a micellar solution, all previous research has assumed that the route to populating the interface with surfactant is through the kinetic adsorption of the surfactant monomer to the surface from the sublayer of solution underneath the surface. This adsorption disturbs the monomer/micelle equilibrium and micelles disassemble to resupply monomer and accelerate the adsorption process. The acceleration in adsorption is an experimentally measured fact, and the standing assumption in the literature is that the disassembly of micelles provides the mechanism to explain the acceleration. However, growing experimental evidence has suggested that aggregates can directly adsorb onto a clean interface, and that this adsorption is a significant reason that the adsorption rate rapidly increases as the bulk concentration increases above the CMC. The objective of this research is to demonstrate experimentally that micelles do adsorb directly from the aqueous sublayer onto the air/water interface, and to construct a model for the adsorption.

In our previous report, we provided conclusive experimental evidence of the direct adsorption route by intercalating a hydrophobic dye into the micelle core, and tracking the rate at which this dye is transported to a clean surface formed in the micellar solution. In this report we detail the framework for modeling the direct adsorption, and dynamic tension experiments to measure the kinetic rate constants of the model. We assume that the aggregate population consists of micelles with σ monomers per aggregate, and that when equilibrium prevails, the monomer (C₁) and micelle (C_σ) concentrations are given by

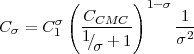
where C_CMC is the critical micelle concentration. At the air/aqueous interface of a micellar solution, exchange of micelles between the bulk and the surface is formulated for the monomer flux j₁ and the aggregate flux j_σ):

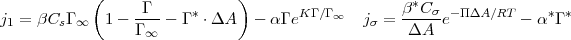
where Γ is the surface concentration of monomer, C_s is the monomer sublayer concentration, α and β are the desorption and adsorption kinetic rate constants for monomer, Γ_∞ is the maximum packing density of monomer, K is the monomer interaction parameter which for polyethoxylates accounts for the repulsion of the head groups in the adsorbed layer, Γ^* is the concentration of adsorbed micelles and C_σ is the sublayer concentration of micelles. In the above, the kinetic scheme for the adsorption of the monomer into the monolayer below the CMC is simply corrected to include the presence of adsorbed micelles in the available area, with ΔA ⋅ Γ^* the reduction in the available area due to aggregates on the surface. The direct adsorption of micelles is formulated using an Arrhenius approach with adsorption and desorption constants α^*,β^*, and the work required to insert the micelle onto the surface given by Π ⋅ ΔA where Π is the surface pressure γ_c - γ. At equilibrium the kinetic framework defines an equilibrium density of aggregates and monomer on the surface as given by:

where the bulk concentrations of monomer and aggregates are related by the monomer/aggregate equilibrium in the bulk. The tension at equilibrium can be computed straightforwardly from the Gibbs-Duhem equation to give an equation of state. The bulk monomer and aggregate concentrations can be eliminated easily from the above set of equations to yield a relationship between the surface and aggregate concentrations at equilibrium. In our application of this theory to the dynamic process of adsorption of aggregates onto a clean surface, we assume that monomer and micelle rapidly equilibrate so that the monomer and micelle surface species are always in equilibrium.

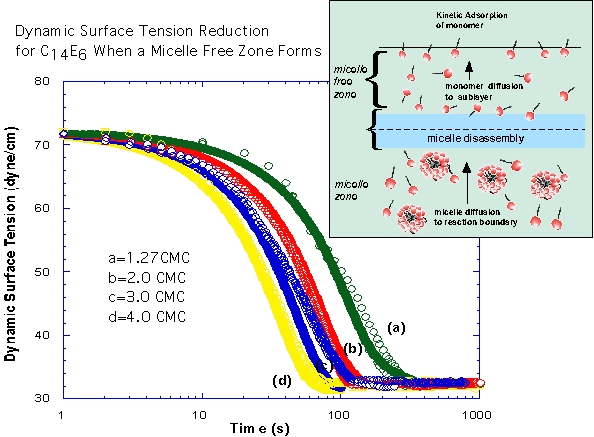
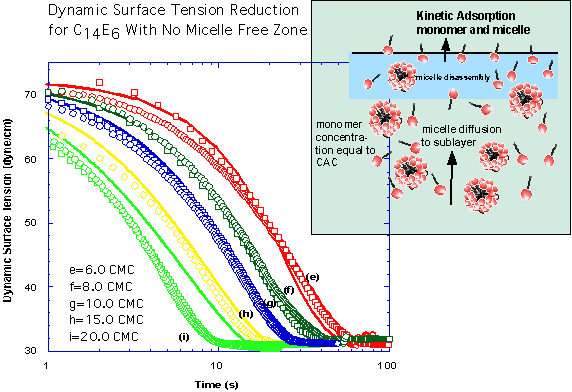
The pendant bubble technique is utilized to measure dynamic surface tensions to obtain the micelle kinetic rate constants. For the polyethoxylated surfactant we have studied, the time scales for adsorption to a clean surface are governed by diffusion of monomer and micelles and are long relative to the slow step for the break-down and re-assembly of micelles in the bulk. As a result, we can assume a quasi-equilibrium in which - at high enough micelle concentrations - the micelles maintain the monomer at the CMC, and only micelles diffuse in the bulk. At lower bulk micellar concentrations, a micelle free zone develops underneath the surface and micelles diffuse to the zone, disassemble and monomer diffuses to the interface. By solving the diffusion equations subject to the specification of the kinetic flux at the pendant bubble surface, the adsorption of monomer and aggregate on the surface can be obtained, and through the equation of state, the dynamic tension obtained. The predicted dynamic tension can then be compared with the measured tension change to obtain the kinetic constants. By using the same procedure for concentrations below the critical micelle concentration where only monomer is present we first obtain the monomer constants: Γ_∞=3.32x10^-6 mole/m², α∕β=2x10^-6 mole/m³, K=7.12 and β=7.0 m³/(mol sec). In the figures below show the dynamic tension measurements and the simulations of the tension reduction for bulk micellar concentrations which form micelle free zones (micellar concentrations below 6 CMC) and higher concentrations that do not form a zone. The simulations were undertaken with the monomer and micelle diffusion coefficients equal to 4x10^-10m²/sec and 1x10^-10m²/sec. The inverse insertion area 1∕ΔA and the micelle adsorption rate constant are taken to be equal to the monomer values, and the desorption rate constant is equal to 7x10^-3sec^-1.