AmericanChemicalSociety.com

1. Introduction:

The objective of the work is the high-resolution 3D characterization and quantification of internal structures for various depositional settings, with the ultimate goal to improve reservoir models and interpretations of depositional processes. The methodology used combines full-resolution 3D ground-penetrating radar (GPR) imaging with statistical analysis of GPR facies and reservoir properties. Specific activities performed in the framework of the grant can be grouped in equipment development, collection of reconnaissance 2D data and full-resolution 3D cubes, and development of processing and analysis algorithms.

2. Data collection:

Ground-penetrating radar data have been collected in a range of depositional environments including a coastal beach ridge along Lake Erie, an eolian dune and the point bar of a meandering river in Michigan, and a braided fluvial deposit in Mississippi. At all these locations reconnaissance data were collected using 2D survey transects at a range of GPR frequencies. GPR data were collected using both pulseEkko100 and ProEX equipment from Sensor&Software and MALA Geoscience respectively. The used frequencies ranged from 50 to 250 MHz depending on the depth of interest and the required detail.

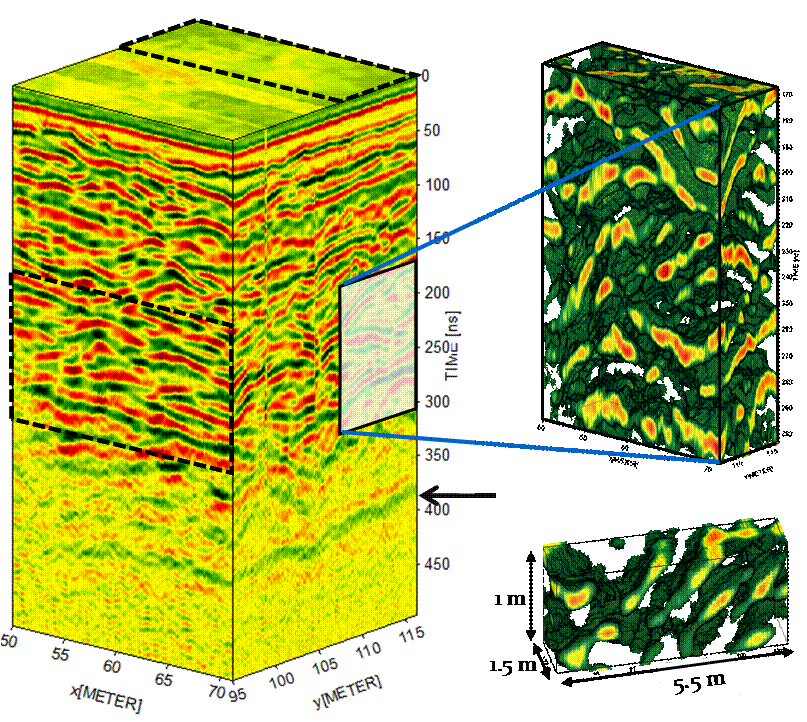
Full-resolution 3D GPR data were so far collected at two test locations (an archeological site and a fractured limestone) to experiment with experimental procedures and field settings. Also, full-resolution data were collected at a site in Mississippi characterized by a combination of meandering and braided fluvial deposits. At this site, we collected non-aliased 3D GPR data (less than ¼ wavelength in- and cross-line spacing) using both 50 and 100 MHz antennas. The step size was set at 0.2m and 0.1m for the 50 and 100 MHz antennas, respectively. Data collection was triggered by an odometer, with positioning controlled by guidance ropes; the position error due to wheel slip was on average less than 1%. The data were processed using a dewow filter (with 100 ns time window) and an AGC gain (window length: 64 ns and scaling value: 1) for visualization. The average below-water table velocities from common-mid-point (CMP) profiles (0.058 m/ns) were then used for time-to-depth conversion. Results of this data collection are shown in Figure 1.

The study site has been thoroughly characterized by past and ongoing research. Our data collection and interpretation benefited from a series of closely spaced cores for grain-size distributions, as well as high-resolution information on hydraulic conductivity based on flowmeter and direct push measurements. The full-resolution 3D GPR cubes collected at this site highlight radar facies characteristic of large scale cross bedding typically found in gravelly fluvial deposits. The correlation lengths are significant according to these geophysical data. The first results of this research have been presented at two international conferences and are being finalized in a manuscript for submission to a peer-reviewed journal.

3. Data analysis:

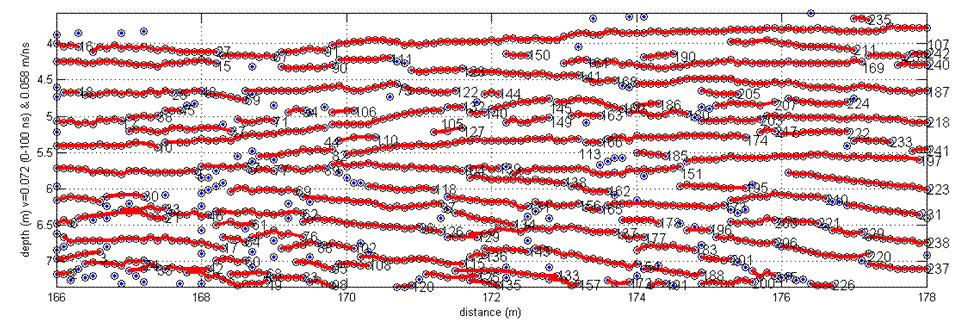
Standard processing of the GPR data, such as the removal of high- and low frequency noise, the correction for surface topography, and the application of gain functions, is performed in ReflexW software. Further analysis of the large data cubes is conducted in MATLAB. To develop a true 3D facies models for the full-resolution data we have developed an algorithm that picks reflections and identifies these as individual layers through information on continuity and dip. Figure 2 shows the results of the algorithm using an example 2D section of data. After identifying the peaks of all positive breaks in each data trace, a random-walk type search is used to identify lateral connectivity in the reflections. This search algorithm builds a library of 3D surfaces that can be further analyzed using statistical and other quantitative methods. In addition, individual layers that are bounded by the identified reflections surfaces can be populated with textural or hydraulic conductivity values for simulation of reservoir properties. This procedure is further discussed in a manuscript that is in final stages of preparation.

4. Ongoing work:

Due to positioning limitations of traditional GPR acquisition strategies, full-resolution 3D data cubes are very time intensive to collect. For example, collection of the data cube in Figure 1 took a full 20 hours. A novel method for real-time fusing of GPR data and positioning information (using a rotary-laser positioning system that acquires cm-accurate coordinates for the moving GPR antennas) was proposed. Due to hardware issues, the task of building this equipment has not been possible during the first phase of the project. Following a 2009 hands-on workshop with the developer of the fusing software, it is anticipated that equipment suite will be completed soon and be available to significantly improve speed of high-quality data collection for final acquisition tasks.

Further analysis of full-resolution data cubes will be a priority for the remainder of the project. The MATLAB code developed to semi-automatically pick 3D layers from the data is instrumental to this task. This code will be improved by directly incorporating amplitude information. Further algorithms will be written to calculate correlation lengths, reflector area, and dip characteristics.

5. Figures:

Figure 1. Three dimensional block of full-resolution GPR data of fluvial braided river deposits collected at Columbus Air Force Base in Mississippi. The data were collected using 100MHz source and receiver antennas with 10 cm in- and cross-line spacing. The arrow marked ~400 ns two-way traveltime refers a clay layer that forms the bottom of the aquifer. Cutouts highlight the 3D nature of depositional structures.

Figure 2. Results of the search algorithm developed in MATLAB shown for a 2D data set of braided fluvial deposits. The algorithm autonomously picks reflections from GPR data (circles) and identifies layers; the algorithm forms the basis for futher statistical analysis of facies.