Reports: G7
47740-G7 Solvent-Temperature Superposition Rules for Predicting the Rheology of Wormlike Micellar Fluids
The goal of this project is to use a combination of atomistic and mesoscale simulations to decipher the relationship between the unique rheological properties of wormlike micelles[1] and the molecular scale structure and interactions in these systems. A description of these modeling efforts is presented below:
(A) Atomistic simulation:
The structure and dynamics in the micellar system consisting of EHAC [erucyl bis(hydroxyethyl) methylammonium chloride] surfactant molecule was studied using atomistic simulations. The molecular dynamics (MD) simulations were carried out using the GROMACS package.[2] The simulated system consisted of 100 EHAC molecules and 54773 water molecules, with 100 chloride ions added to maintain charge neutrality. The initial structure was energy minimized using the steepest descent method, followed by a constant NPT (number of particles, pressure and temperature) MD simulation run for 40 ns.
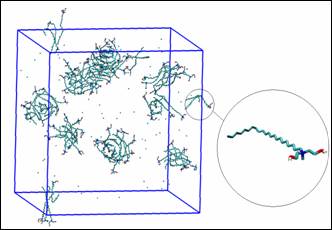
Fig. 1. Configuration of the EHAC molecules after
40 ns of MD NPT simulation (water molecules
have been removed for clarity). Inset
shows an EHAC molecule.
As seen from Fig. 1, the EHAC
molecules were observed to form aggregates of different sizes. The Gromos clustering algorithm[3] in
GROMACS was utilized to quantify this aggregation behavior of the EHAC
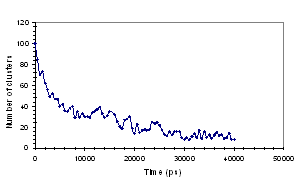
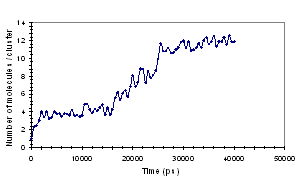
molecules in solution, the results are shown in Fig. 2.
(a) (b)
Fig. 2: Aggregation of EHAC molecules as shown by (a)
Time dependence of the number of clusters and (b) Time dependence of the average
number of molecules per cluster.
(B) Mesoscale simulation:
In order to capture the
rheological properties of the wormlike micelles as measured in experiments, we
need to simulate the systems on much longer length and time scales than
possible using atomistic simulations.
In this project, we have decided
to use the multi-particle collision dynamics (MPCD) method[4] for this purpose. The coarse grained models used in these
mesoscale simulations will be developed from the atomistic simulations as
described above. As a first step, we are
currently developing a simulation code for implementing the MPCD method. A brief description of this simulation method
and the results from our calculations are presented below.
MPCD Method:
In the MPCD method, the solvent
is described as a collection of N
point particles. These particles are
assumed to interact at discrete time intervals by collision events and are
assumed to undergo free streaming motion in between these collisions. The dynamics of the solvent particles is thus
implemented in two steps:[5]
(1) Streaming step:
where
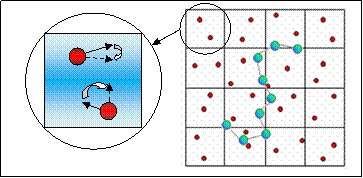
Fig. 3: Schematic illustrating the partitioning of the box into cells
containing the solvent particles and one bead-spring polymer chain in MPCD
simulation. Inset shows the rotation of
the relative velocity of every solvent particle in a MPCD cell.
(2) Collision step: The
particles are first sorted into cells (see Fig. 3). The relative velocity (with respect to the center
of mass velocity in that cell) of each of the particles in a cell is then
rotated by a chosen angle:
where
A hybrid approach is used for simulating
the dynamics of a solution containing a solute that is dissolved in the mesoscopic
solvent as described above. In this
case, the free streaming step is replaced by usual MD simulation for the
solvent and solute particles to account for the specific interactions between
the solute and the solvent whereas the solvent-solvent interactions are captured
via the collision step as described above.
The initial simulation system studied
contained 326769 solvent particles in a box of dimensions 32x32x32 and at a temperature
of 1/3. The angle of rotation was
π/2 for all cells. Furthermore, the
system contained one colloidal molecule (radius = 3σ, mass = 250) that
interacted with the solvent molecules via the Lennard-Jones (LJ) potential (all
values are in reduced LJ units). In the
simulation, 50 MD steps were carried out between successive collision steps and
the system was equilibrated for 20,000 MD steps. In order to validate our code, the normalized
velocity autocorrelation function (VACF) of the solute particle was calculated.
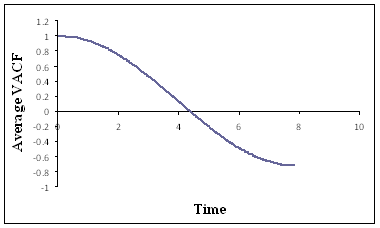
Fig. 4: Normalized VACF of the colloidal particle
averaged over 10 blocks
The VACF shown in Fig. 4
is qualitatively similar with that in the literature but differs from it
quantitatively.[7] Currently this issue is being
investigated. Once this issue is resolved
and the code is validated, a similar test will be performed for the MPCD code
for a polymer solution; the validated code will then be used for studying the
rheology of the wormlike micellar systems.
Impact of the
research on the PI and the graduate student
The PI (Khare) has a strong track
record of atomistic level simulations of polymeric systems as well as nanoscale
transport phenomena. The ongoing work on
this project in the area of MPCD simulations will allow the PI to expand his
research portfolio to mesoscopic modeling techniques. The graduate student (Govind Hegde) working
on this project is receiving multidisciplinary training in the areas of
chemical engineering, mesoscale and atomistic simulation methods and rheology
of complex fluids.
References:
[1]
Siriwatwechakul,W.; LaFleur, T.; Prud'homme, R.K.; Sullivan, P.; Langmuir, 20, 8970-8974 (2004).
[2] 2. Hess,
B.; Kutzner, C.; van der Spoel, D.; Lindahl, E.; J. Chem. Theory Comput.
4, 435-447, (2008).
[3] Daura, X.; Gademann, K.; Jaun, B.; Seebach, D.; van
Gunsteren, W. F.; Mark, A. E.; Angew. Chem. Int. Ed. 38, 236-240, (1999).
[4] Kapral, R.; Adv. Chem. Phys.; 140, 89 (2008).
[5] Malevanets, A.; Kapral, R.; J. Chem. Phys. 110,
17, 8605-8613, (1999).
[6] Ihle, T.; Kroll, D. M.; Phys. Rev. E., 63,
020201, (2001).
[7] Malevanets, A.; Kapral, R.; J. Chem. Phys. 112,
17, 7260-7269 (2000).
and
denote the position and velocity of particle i at time t.
is the center of mass
velocity and
is the rotation matrix. The rotation is done by a fixed angle α
about a randomly oriented rotation axis.
Same rotation is applied to all particles in one cell but the rotations
in different cells are independent of each other. To ensure Galilean invariance for the
simulation, a random lattice shift for the cells is applied before each
collision step, to change the neighborhood of the particles.[6]
