AmericanChemicalSociety.com

The original goal of this project was to develop real-time path integral methods to incorporate nuclear quantum effects into ab initio molecular dynamics simulations. Such methods could be used, for example, to compute reaction rate constants using on-the-fly electronic structure theory. While such methods still hold promise, they are extremely computationally demanding, and this prohibits extensive algorithm development at ab initio levels of theory. At the same time, we are skeptical about whether density functional theory (DFT), the workhorse electronic structure model for ab initio molecular dynamics, is sufficiently accurate and reliable for calculating the reaction barrier heights needed to determine reaction rates.

To address these problems, we have worked to develop new "long-range corrected" (LRC) density functionals that partially eliminate DFT self-interaction errors. At the same time, we have endeavored to construct a simple model potential that can be used to test and improve path-integral algorithms. To this end, we began to examine interaction potentials for the aqueous electron (e_aq^–), which has long been used as a model system for path integral calculations. We discovered that LRC-DFT methods, though developed with other purposes in mind, are well-suited to the description of solvated electrons, and the hydrated-electron model that we originally developed in order to test path integral algorithms appears to be significantly more accurate than previous e_aq^– models. This model moreover predicts some previously unseen behavior in simulations of the bulk aqueous electron, and is therefore interesting enough to merit serious investigation in its own right. As such, e_aq^– simulations evolved into a central aspect of the project.

This report details the progress that we have made over the two-year funding period.

(1) Development and testing of long-range corrected (LRC) density functionals

As a result of spurious self-interaction in DFT, the exchange–correlation energy of a one-electron system is not zero, and this artifact of approximate density functionals causes DFT to overstabilize systems containing singly-occupied orbitals, such as transition states in chemical reactions, or radical anions. This problem is absent in uncorrelated Hartree–Fock calculations, because the Hartree&nbash;Fock exchange operator precisely cancels the self-interaction present in the Coulomb potential. Efforts to incorporate full Hartree–Fock exchange into DFT calculations have produced poor results, however, because an appropriate correlation functional for use with Hartree–Fock exchange is unknown.

In this work, we have pursued a different approach, in which Hartree–Fock exchange is incorporated only asymptotically, using the long-range part of a Coulomb operator that has been separated into short- and long-range components. Short-range interactions are treated with traditional DFT exchange, although the exchange functionals must be derived using the short-range Coulomb operator. We have implemented short-range versions of the Perdew-Burke-Ernzerhof (PBE) and Becke exchange functionals within the Q-Chem electronic structure program.

Relative to the original functionals, the new LRC-DFT functionals contain two adjustable parameters: a Coulomb attenuation parameter that controls the partition of the Coulomb operator into short- and long-range components, and the fraction of Hartree–Fock exchange that is incorporated into the short-range part of the exchange functional. We optimized these two parameters by means of exhaustive benchmarking of both ground-state properties and electronic excitation energies calculated using time-dependent DFT. (Excitation energies, especially for Rydberg and charge-transfer excitations, are extremely sensitive to the long-range behavior of the exchange–correlation potential.) The result is a density functional whose performance for ground-state properties and localized valence excitation energies (nπ*, ππ*, πσ*, etc.) is comparable to the performance of the workhorse hybrid functional PBE0, but whose mean error for charge-transfer excitation energies (~0.3 eV) is reduced by an order of magnitude relative to PBE0. This is the first density functional to offer a balanced description of both valence and charge-transfer excitation energies, and we expect it to see significant use in the near future.

(2) Development of a new model for simulation of the aqueous electron, e_aq^–

Because LRC-DFT is rigorously free of self-interaction error in the long-range limit, it is ideally suited for the description of solvated electrons, where the unpaired electron resides largely outside of the valence orbitals of the solvent molecules. LRC-DFT electron binding energies calculated for small (H₂O)_n^– clusters are in good agreement with benchmark CCSD(T) results. By performing LRC-DFT calculations on H₂O^–, we obtain a one-electron pseudopotential for the singly-occupied molecular orbital, φ, according to

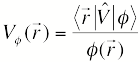
When combined with an accurate, polarizable force field for water, this pseudopotential affords a one-electron Hamiltonian that can be used for quantum molecular dynamics simulations of e_aq^– or (H₂O)_n^–. Comparison to ab initio benchmarks in clusters demonstrates that the new model is significantly more accurate than earlier, non-polarizable models, for both electron binding energies and relative conformational energies.

Encouraged by this accuracy, we have begun to perform simulations of aqueous electrons in bulk liquid water. These simulations reveal surprising, qualitative differences with respect to older, non-polarizable models. For example, the figure below shows the electron–hydrogen radial distribution functions, g(r), calculated with both polarizable and non-polarizable models.

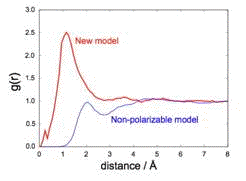
Non-polarizable models exhibit a minimum in g(r) around 2.8 Å, corresponding to a well-defined, four-coordinate first solvation shell. In simulations performed using the new model, however, this minimum is washed out by rapid water dynamics around the excess electron. This prediction is consistent with experimental measurements of a large, positive entropy of solvation for e_aq^– and a short (< 100 ps) residence time for water molecules in the first solvation shell. 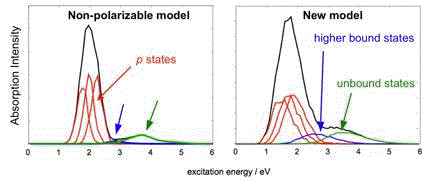To the best of our knowledge, these experimental features have not been explained, or even reproduced, by any other theoretical simulations. The new model is also the first to reproduce the high-energy tail of the experimental absorption spectrum of e_aq^–, which (according to the calculations) arises from excitations out of the s-like ground state into delocalized states that are not well described by non-polarizable models.

Work is ongoing in our group to probe the structure and spectroscopy of the aqueous electron using the new model.