AmericanChemicalSociety.com

Two projects were carried out under PRF funding, one of which is an investigation into the high-strain-rate behavior of dilute polymer solutions, and the second is the implementation of a method for including chain non-crossability into Brownian dynamics simulations.

Project 1: High-Strain-Rate Behavior of Dilute Polymer Solutions

The slow dynamics of polymers in dilute solution are well described in the linear viscoelastic regime by the Rouse-Zimm theory which coarse-grains a polymer into a sequence of frictional beads connected by Hookean (or linear) springs.¹ What is left unresolved by this theory is the way in which the coarse-grained bead-spring model breaks down at shorter time and distance scales than those for which linear 'springs' can capture the configurations of the chain. One expects that at short times, the viscoelastic response should be controlled by motions of small groups of bonds and should not be describable by a coarse-grained bead-spring model. Nevertheless, very surprisingly, experiments by Schrag, Lodge, and coworkers^1,2 have shown that the Rouse-Zimm bead-spring chain model can actually describe reasonably well the entire frequency range of dilute polystyrene or polyisoprene chains—even at frequencies high enough that single springs are expected to be strongly excited. This is true as long as the number of springs is chosen so that each spring represents a sub-molecule of molecular weight 4500 for the case of polystyrene and 2400 for polyisoprene.²  As an explanation, it has been suggested that torsional barriers to bond rotation might confer a large 'dynamic stiffness' to polymers that slows down modes requiring fast bond motion causing their relaxation to overlap with that of slower collective modes that can be represented by a Hookean spring in a bead-spring model.^3,4

To test such ideas and to better understand the mechanism of energy dissipation at high frequencies in dilute solutions, we conducted a Brownian dynamics study of a linear polymer chain in which the beads represent individual backbone atoms. We used stiff Fraenkel spring forces ⁵ to maintain the distance between atoms near 1.53 , bending forces to enforce tetrahedral bonding with a bending angle of 109⁰ 47', and torsional forces to create realistic barriers to torsional transitions. Brownian forces were introduced through white noise. The simulations showed that both the bending and torsional potentials slowed down the contributions of local relaxation modes, bringing the relaxation of short chains close to single exponential behavior. Thus, the local modes in dilute polymer solution relax at rates similar to that of a coarse-grain mode that can be represented by single Rouse-Zimm spring, encompassing the motion of dozens of backbone bonds. Our results in qualitative agreement with measurements of birefringence relaxation and the notion of a "dynamical Kuhn length".³ These results are significant in showing the limits of a coarse-grained bead-spring model for polymers, and in defining how bending and torsional potentials affect the viscoelastic spectrum.  Such results carry implications for local polymer dynamics more generally, and have connections to problems of solvent molecular transport through polymers, and to lubrication flows and tribology.

Project 2: Chain non-Crossability in Brownian Dynamics Simulations

In a second project, the non-crossability of polymer chains was incorporated into Brownian dynamics simulations through development of a repulsive spring potential that prevents springs from passing through each other.  This allowed us to impose "entanglements," or chain non-crossability, into coarse-grained Brownian dynamics simulations.  This new method was then applied to the case of an isolated polymer molecule in a shear and extensional flow, for both good and poor solvent qualities.  The simulations showed that chain non-crossability had little effect on polymer stretching dynamics, but we found that solvent quality had a very large effect.  We also found, surprisingly, that chains with both a long range spring-spring repulsion and a short-range bead-bead attraction chosen to cancel the effect of spring-spring repulsion on the no-flow coil size, do not deform much under strong shear, while the chains with no interactions (and the same no-flow coil size) do deform significantly under shear.  These results show that chain deformation under shear is controlled not just by overall solvent quality, but by the distance dependence of the chain-chain interactions.

Impact on Careers of Advisor and Students

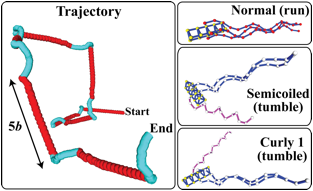
Three Ph.D. students have been supported significantly by the grant.  Sean Holleran, who worked on the first projected, graduated with a Ph.D., and has become a Lecturer in Chemical Engineering at the University of Pennsylvania.  Semant Jain, who worked on the second, also graduated and is now a scientist at Praxair Corporation.   A third Ph.D. student, Indranil Saha Dalal, is still in the research group.  All three were greatly benefitted by the financial support; the first two landing their positions after giving research talks based on the work done under the PRF grant. In addition, two self-funded undergraduate students, Nick Orichella and Jeremy Shum, worked on the second project, and gained experience in research.  In addition, the simulation methods developed during this project have launched me in a new research direction, that of simulating the motility of bacteria and artificial swimmers.  The figure below illustrates the use of the tools developed for polymer simulations under the PRF grant to the problem of swimming of an E. Coli bacterium, carried out by Nobu Watari, a current Ph.D. student.  I am seeking to fund this new work through a proposal to the Department of Energy.

Fig. 1.  Typical trajectory of a modeled cell in run-and-tumble motion (left) and

snapshots of cell conformations in different states during the motion (right).

Bibliography

1. Amelar, S.; Eastman, C. E.; Morris, R. L.; Smeltzly, M. A.; Lodge, T. P.; Meerwall, E. D. V. Macromolecules 1991, 24, 3505 - 3516.

2. Peterson, S. C.; Echeverria, I.; Hahn, S. F.; Strand, D. A.; Schrag, J. L. Journal of polymer science: Part B: Polymer physics 2001, 39, 2860 - 2873.

3. Larson, R. G. Macromolecules 2004, 37, 5110-5114.

4. Fixman, M. Journal of chemical physics 1978, 69, (4), 1538 - 1545.

5. Symeonidis, V.; Karniadakis, G. E.; Caswell, B. Computing in science and engineering 2005, May/June, 39 - 46.