Reports: G6
47880-G6 Molecular Basis of Tetrahydrofuran-Induced Enclathration
The principal goal of this project is to understand the role of tetrahydrofuran (THF) in promoting the enclathration of methane. A molecular-scale understanding of this process requires understanding the physics of hydration and how additives such as THF change the solubility of a third component (methane). The solubility is quantified by the excess chemical potential, a quantity that is the target of our theory and simulation efforts. Below we summarize the main achievements in developing the theory and simulation and the scientific insights that we have obtained thus far.
The excess chemical potential of the solute in water can be separated into (1) a chemical term, arising due to the interaction of the solute with water molecules within the defined coordination sphere (the inner-shell), (2) a packing contribution, accounting for forming a solute-free coordination sphere (the observation volume) in the solvent, and (3) a long range correction, accounting for the interaction of the ion with the solvent outside the coordination sphere. The long-range correction usually admits a simplified (mean-field) description.
To obtain insights into local (chemical) solute-water interactions on hydration, we recast the chemical term as a sum over coordination states. The nth term of the sum depends on the probability of observing n water molecules in the observation volume and the free energy of assembling the n water molecules around the solute in the presence of the outer-shell solvent. Each step-wise increment in the coordination number more fully accounts for the chemical contribution. This molecular aufbau approach was used to interrogate the thermodynamic importance of various hydration structures X[H2O]n of X(aq) (X= Na+, K+, F-) within a classical molecular mechanics framework. For this initial study we chose to study the hydration of ions because of two reasons: (1) the intrinsic scientific interest and conceptual simplicity of ion hydration, and (2) ion-water interactions define the upper limit of solute water interaction energies and this system thus provides a rigorous test of theories in the strong interaction limit.
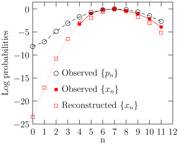
The most important insight emerging from this study was the identification that states with n less than (and at best equal to) the most probable coordination state ñ account for all of the chemical term and evince the role of the solute in drawing water molecules into the coordination sphere. For states with n > ñ, the influence of the solute is tempered and changes in coordination states due to density fluctuations in water also appear important. The identification of the role of water density fluctuations at the size scale of the coordination volume is a significant conceptual advance in understanding hydration phenomena. Fig. 1 below shows the results from this analysis for K+ (aq).
Fig. 1: The ion-free water occupation probabilities {pn} and the coordination states of the ion {xn} are shown. Beyond n=7, the most probable coordination state, the coordination states are sensitive to the density fluctuations in the medium. The coordination states reconstructed on the basis of the theory we developed is in excellent agreement with the observed distribution where the data is available.
The occupation number distribution {pn} of water molecules in the solute-free observation volume defines the density fluctuations at the size scale of the observation volume. The p0 member of this set, that is the probability of emptying the observation volume of all water molecules, specifies the packing contribution to hydration. For cavity sizes about the size of a water molecule (3 Å), p0 can be directly accessed from simulations. But excessively long simulations would be required to observe the n = 0 state for cavity sizes that are large enough to enclose a molecule such as THF. Inspired by the expanded-ensemble method, we have implemented a biasing method that helps extract the low probability occupancy states in simulations.
Corresponding to the n state, the canonical partition function of the entire system is Qn(N,V,T), where N is the total number of particles in the system of volume V at a temperature T. The probability that the system samples configurations resulting in the n-state is Pn = C Qn, where C is a normalization constant. Thus Pn/Pm = Qn/Qm. The idea in the biased sampling approach is to introduce weights wn to define a new probability of the n-state P'n = C Qn exp(wn). Thus
P'n / P'm = Qn/Qm exp(wn – wm).
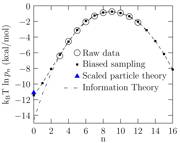
Initially the weights are set proportional to the probabilities of the states obtained in a short simulation. Of course, not all states are sampled. Nevertheless, once the biases are applied, more and more of the low probability states are uncovered with periodic updating of the weights. This iterative scheme of updating the weights is continued and the ratio P'n/P'm is driven towards unity. The original probabilities are then recovered from the final weights. The advantage of biasing is that we sample all the states uniformly and with the same statistical confidence. The results of the biased simulation approach are shown in Fig. 2.
Fig. 2. The occupation probabilities of a cavity of radius 4 Å in bulk water. Observe that the state n=0 is not observed in a direct simulation. The p0 value is readily obtained by the biased sampling technique and the numerical agreement with scaled particle theory is excellent. In contrast, information theory, an approach that has been often used before, predicts a quantitatively inaccurate result.
Currently, we are applying the biased simulation technique to study the hydration of molecules such as CH4, CF4, and neopentane (C(CH3)4). Using the same technique, we are studying the solubility of methane in the aqueous electrolytes. These studies will form the basis of our studies on the hydration of THF and on the effects of THF on the solubility of CH4.