Reports: AC6
47444-AC6 Semiclassical Correlation Energies of Atoms and Molecules
PRF REPORT
Eric J. Heller
Department of Chemistry and Chemical Biology, Harvard University, 12 oxford Street, Cambridge MA 02138
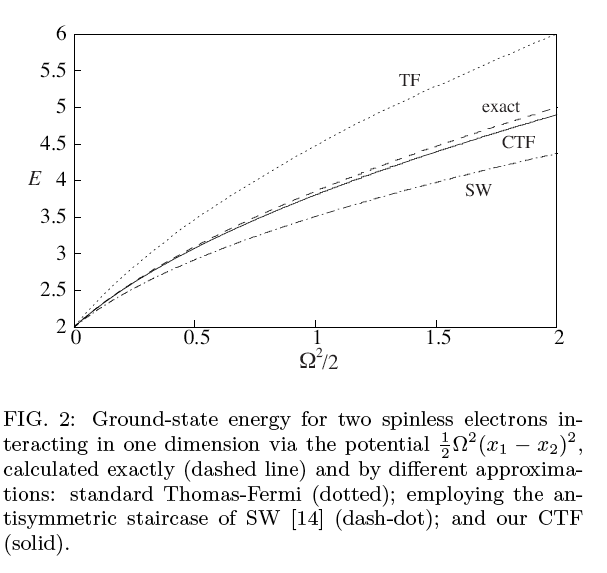
We (E. J. Heller, Adam Wasserman, and Brian Landry) have succeeded in developing a new and very promising semiclassical method allowing determination of accurate ground-state energies for many-electron systems. The method borrows its semiclassical character from Thomas Fermi theory (TF), but improves upon it by including exchange-correlation effects, at least approximately. We have illustrated our method (CTF) on simple models of 1D-interacting electrons, showing that it yields dramatic improvements over TF, particularly in the strongly-correlated regime.
Determining accurate ground state energies of matter at all levels of aggregation has remained one of the major challenges of computational chemistry and physics for the last 80 years.
Solving numerically the N-electron Schroedinger equation is implausible for systems containing more than a few electrons, but ingenious ideas have been developed to find approximate solutions
In the midst of recent resurgent interest in the semiclassical origins of Density Functional Theory this work amounts to putting forth a new idea inspired by an old method to calculate ground-state energies of many-electron systems.
The genesis of the idea is the observation that the classical density of states obtained by tracing over the classical Hamiltonian gives and accurate redition of the quantum density of states, never off by more than one quantum state. This trace is over the full interacting Hamiltonian, and thus is cognizant of all the interparticle interactions.
We however encounter a significant problem, in that the classical density of states tracks closely the quantum density of states of all symmetries, whereas the Fermions systems of interest account for only about 1/N! fraction of those, because only total antisymmetric eigenstates can be counted. This men's that if, separately, the order number of the first antisymmetric state is known (e.g. the 43rd state is he first one obeying fully antisymmetric Fermionic statistics) that we have a very quick and accurate method indeed foe even very strongly correlated systems; perhaps one should say perhaps especially such systems.
We began by focusing attention on the various ways in which different methods account for Pauli's principle, because the central result of our work is the observation that accurate ground-state energies can be obtained within a semiclassical context rather than from the start as present-day methods do.
The correlation energy for an N-electron system is not readily accessible from semiclassical Wigner-Kirkwood expansions or related techniques These methods are normally employed to obtain approximate density functionals for the Kohn-Sham density matrix, from which all but the `correlation' pieces of the energy can be easily constructed. It is the N-body Green's function, rather than the Kohn-Sham one, that must be used as input to obtain approximate correlation energies. Our CTF results suggest that this route to correlation energies is indeed worth exploring, and is worthwhile fruit of the PRF support we have gratefully revived.
This work has now been accepted to Physical Review Letters for publication (B. R. Landry, A. Wasserman, and E. J. Heller, Semiclassical ground-state energies of many-electron systems, in review Phys. Rev. Lett., (2009).) We are very proud things have gone this successfully, and to have tehe recognition, but we have a way to go: the discoveray of a reasonable algorithm to estimate the order of appearance of the first totally antisymmetric state among the spectrum of the states. Fig. 2 from the paper is shown below, demonstrating the superiority of the method: