AmericanChemicalSociety.com

The compounds of the least electronegative metals from groups 1 and 2 with the more electronegative metals and metalloids, commonly known as Zintl phases, have attracted much interest over the years. In particular, very recently, detailed studies on such ternary antimonides with complex structures, such as Yb₁₄MnSb₁₁ and Ca_xYb_1–xZn₂Sb₂ have shown that Zintl phases exhibit high thermoelectric figures of merit (ZT) and therefore, can be used as materials for direct thermal-to-electric energy conversion. As the thermoelectric properties are closely related to the crystal structures, the search for new pnictides with complicated structures, has gained renewed interest.

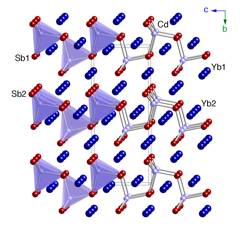
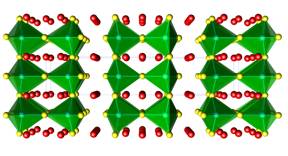
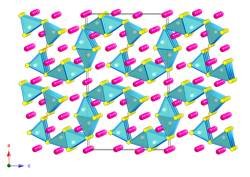
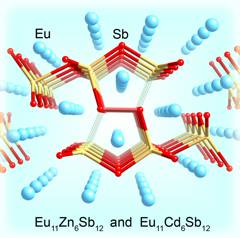
The research in our group has been inspired by these recent discoveries, which motivated us to conduct systematic studies of the fundamental trends in electronic and crystal structures of alkaline- and rare-earth metals antimonides and bismutides. A number of new Zintl phases have already been synthesized and structurally characterized, including Yb₂CdSb₂ and Ca₂CdSb₂ (Figure 1), Eu₁₀Cd₆Bi₁₂ (Figure 2) and Ba₁₁Cd₈Bi₁₄ (Figure 3), Eu₁₁Cd₆Sb₁₂ and Eu₁₁Zn₆Sb₁₂ (Figure 4). As a part of these ongoing systematic investigations in the A–M–Pn systems, where A = divalent alkaline- or rare-earth metals, M = Mn, Zn, Cd, Pn = pnicogen, we embarked on studying the Ba–Cd–Sb phase diagram. For a long time, there have been known only two compounds BaCd₂Sb₂, and BaCdSb₂, but we recently discovered the new complex Zintl phase Ba₁₁Cd₆Sb₁₂. Herein, we describe the continuation of our studies, and report on the synthesis, structural characterization and electronic band structure calculations of the new Zintl phase Ba₃Cd₂Sb₄. It crystallizes with a complex monoclinic C-centered structure, which is composed of Cd centered Sb tetrahedra that share edges. Attempts to synthesize analogs of the title compound resulted in four mixed-cation Ba_3–xA_xCd₂Sb₄ phases, where A = Ca, Sr, Eu, Yb.

Crystals of the new ternary compound Ba₃Cd₂Sb₄ were obtained from a reaction of Ba, Cd and Sb metals in Pb flux. Analogous reactions were also undertaken in the systems A–M–Pn, where A = Ca, Sr, Eu, Yb; M = Zn, Cd; and Pn = Sb, Bi, but did not yield any compounds, isostructural with Ba₃Cd₂Sb₄. Successful were only reactions with mixed A–Ba cations, which produced Ba_3–xA_xCd₂Sb₄ solid solutions with narrow homogeneity ranges.

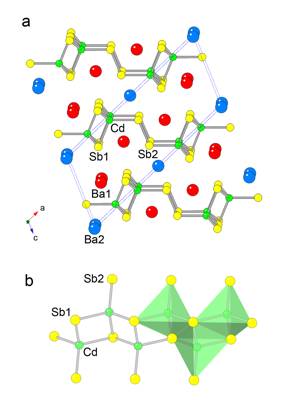
The crystal structure of Ba₃Cd₂Sb₄ was established by X-ray diffraction. It is best described as a polyanionic [Cd₂Sb₄]^6– sub-lattice made up of CdSb₄ tetrahedra and Ba²⁺ cations enclosed between them, as shown in Figure 5. The CdSb₄ tetrahedra share corners to form [CdSb₃] chains, running along the crystallographic b-direction. Similar structural fragments are found in many Zintl phases as well, for example [AlAs₃]^6– in Ca₃AlAs₃, and[SnP₃]^5– in Sr₅Sn₂P₆, to name a few. In Ba₃Cd₂Sb₄, the [CdSb₃] chains are "dimerized" through shared vertices and edges, resulting in [Cd₂Sb₄] double chains (Figure 5b). The latter are further connected to the neighboring chains via exo-Sb–Sb bond to form two-dimensional layers. The [Cd₂Sb₄]^6– layers propagate parallel to the [20] plane and are separated by the large Ba²⁺ cations (shortest interlayer distance greater than 4.7 ). The Cd–Sb distances fall in the narrow range from 2.9125(4) to 2.9531(5)  and the Sb–Cd–Sb angles vary between 101.95(1)° and 113.36(2)°. These metric parameters are comparable to the ones reported for other intermetallic compounds with structures based on CdSb₄ tetrahedra. Almost all interatomic distances in the substitution derivatives Ba_3–xA_xCd₂Sb₄ (A = Ca, Sr, Eu, Yb) are systematically shorter than those in Ba₃Cd₂Sb₄, following the contraction of the unit cell volume. Notable exceptions are the Sb–Sb bonds, which seem to elongate upon mixing of the larger Ba²⁺ with the smaller Ca²⁺, Sr²⁺, Eu²⁺, and Yb²⁺ cations.

The Sb–Sb distance in Ba₃Cd₂Sb₄ is 2.8114(8) , appreciably shorter than the 2.908  contacts in elemental Sb. This is not unusual given that d_Sb–Sb on the order of 2.8  are well known for compounds with related exo-bonded structural elements, such as Ba₁₁Cd₆Sb₁₂, as well as some simpler binaries – KSb and Rb₅Sb₄. Noteworthy, as mentioned above, is the fact that the Sb–Sb distances are elongated on shortening the unit cell axes – for example, in Ba_2.37(1)Sr_0.63Cd₂Sb₄, where the volume change is most significant, ca. –2.5%, the Sb–Sb bonds are 2.8291(8) , almost 0.8% longer compared to the Sb–Sb bonds in Ba₃Cd₂Sb₄. Similar subtlety of the bonding was previously discussed for the pair of isostructural compounds Sr₁₁Cd₆Sb₁₂ and Ba₁₁Cd₆Sb₁₂, where regardless of the large volume change, d_Sb–Sb remains virtually unchanged. All of the above is indicative of a very strong covalency of the Sb–Sb interactions.

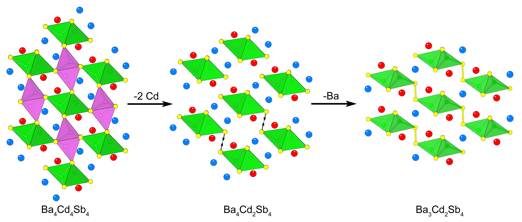
A different description of the Ba₃Cd₂Sb₄ structure can be proposed once its close relationship with the ubiquitous TiNiSi structure type is recognized. This structure boasts a polyanionic 3D framework of corner- and edge-shared tetrahedra and cations residing within its channels. Using an imaginary cutting and pasting, as schematically illustrated in Figure 6, the structure of Ba₃Cd₂Sb₄ can be conveniently derived from that of the hypothetical BaCdSb compound (TiNiSi type), reformulated for convenience as Ba₄Cd₄Sb₄. It requires removing a selected half of the CdSb₄ tetrahedra from the framework, in a way that isolated [Cd₂Sb₄]^8– chains of edge-shared tetrahedra are left behind. Next, through a small distortion, these fragments are brought closer together and joined via adjacent Sb apexes to form <[Cd₂Sb₄]^6– layers, with exactly the same topology as the layers in Ba₃Cd₂Sb₄. Finally, due to the formation of Sb–Sb exo-bonds and the changed crystal packing requirements, one of the Ba²⁺ cations becomes redundant and needs to be removed. The outlined imaginary transformations accounts for not only the structure, but also the composition of the title compound according to the balanced equation:

Ba₃Cd₂Sb₄ = Ba₄Cd₄Sb₄ – 2«Cd – Ba

Last, following this description of structural relations, and before moving on to a more in-depth analysis of the electronic structure, it is useful to discuss the electron count using the Zintl rules. Following them, Ba₃Cd₂Sb₄ should be a charge-balanced Zintl phase according to the formulation (Ba²⁺)₃[(4b-Cd^2–)₂(3b-Sb⁰)₂(2b-Sb^1–)₂].

Figure 1

Figure 2

Figure 3

Figure 4

Figure 5

Figure 6