Reports: B6
47262-B6 Examining Hydrodynamic and Solubilization Properties of Micelles Formed by Chiral Amphiphiles with NMR
In the study of bile acid micelles, a wide range of critical micelle concentration (cmc) values have been reported. Recently, through NMR chemical shift data,we were excited to cleanly observe two discrete aggregation events: one at 7 mM and a second at 14 mM cholate in basic (pH 12) solutions. We have extended our work to include deoxycholate and also to include NOE measurements. Through these measurements, we are gaining a better structural understanding of these complex but powerful micelle systems.
i. Towards a unified understanding of bile acid aggregation
Deoxycholate has one fewer –OH group than cholate, and under similar conditions, is known to have a lower cmc. Using chemical shift analysis, we have been able to measure aggregation in deoxycholate where we observe again two well resolved stages.
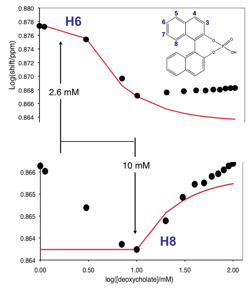
Figure 1. Representative chemical shifts of the probe molecule BNDHP (inset) are shown as a function of the deoxycholate concentration. Each series is mathematically modeled (red lines) with a single cmc to highlight that protons H6 and H8 report on different stages of aggregation.
(Notice that the deoxycholate chemical shift titrations are very information rich. A single-cmc model accurately accounts for the early data for BNDHP-H6 (top) but fails exactly at the onset of the cmc observed with BNDHP-H8.)
Cholate and deoxycholate appear to follow the same fundamental stages of aggregation. The first stage ( 7 mM in cholate, ~3 mM in deoxycholate) results in a transient primitive aggregate consistent with an antiparallel bile acid dimer. The second stage (14 mM for cholate, 10 mM for deoxycholate) forms a persistent primary micelle that seems to preserve the structure of the primitive aggregates which compose it.
Our data show two closely spaced but distinct aggregation stages for both deoxycholate and cholate. We believe this is highly significant since it provides a framework for unifying seemingly disparate reports of cmc values that have persisted in the literature for decades. Specifically, different experimental methods and analyses may be sensitive to the primitive or primary cmc's only, or even to their average values. Yet it is also necessary to try to understand higher order aggregation which some assert is continuous and others assert is characterized by a highly discrete cmc. We will focus significant effort towards trying to understand the nature of higher order aggregation.
ii. A structural model revealed for chiral discrimination of R,S-BDNHP
We are pleased to report major progress in understanding the structural mechanism for how bile micelles are able to differentially solubilize the enantiomers of some analytes.
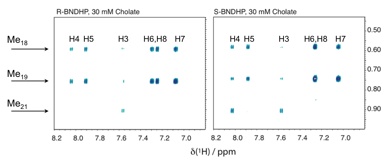
First, 2D-NOE data demonstrate that both R- and S-BNDHP (inset in Fig. 1) utilize the same hydrophobic binding pocket in cholate, featuring strong interactions between the cholate methyl groups and the BNDHP naphthyl rings. Nearly identical data have been obtained for cholate (Fig. 2) and deoxycholate (not shown) micelle systems.
Figure 2. Two-dimensional NOE data (600 MHz) show that R- and S-BNDHP have the same through-space interactions with the methyl groups of cholate.
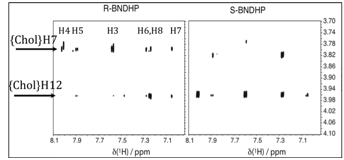
Next, in Figure 3 we show a different portion of the 2D-NOE data with cholate in which R- and S-BNDHP have exactly inverted NOE patterns with the edges of the bile acid (H7 and H12 of cholate are on opposite edges of the micelle aggregate). This requires that R- and S-BNDHP interact with the hydrophobic pocket from opposite edges. Importantly, deoxycholate also exhibits edge-inverted NOEs for R vs S-BNDHP (not shown).
Figure 3. 2D-NOE data for R,S-BNDHP in the presence of 80 mM cholate.
Differential edge attack of binaphthyl atropisomers on bile salt dimeric units represents what we believe to be the first structural explanation for the mechanism of chirally selective solvation. However the NOE data are sparse so that we have not restrained the exact position of R-and S-BNDHP enantiomers when docked to their respective opposite edges, a major unresolved question in developing this model that we are pursuing.