AmericanChemicalSociety.com

The present project investigates aqueous liquid foams, which are known as non-Newtonian, viscoleastic materials. However, they can also be described through their microstructure, i.e., the arrangement and geometry of bubbles. Long known to influence strain response and plastic deformation, microstructure is particularly crucial when studying failure (cracks), where a void propagates through the foam. We apply a well-defined driving pressure to one end of a rectangular channel containing one layer of bubbles (quasi-two-dimensional foam) with well-ordered, monodisperse bubbles in order to generate such a void crack. In our experiments, we take high-speed movies and analyze the resulting images.

In the project proposal and previous reports, we highlighted the need to study two modes of fracture:  ductile, finger-like void propagation and brittle, cleavage-like fracture. Our main findings since the last progress report concern the distinction between modes, the transition between them, and the existence of critical velocities for both modes.

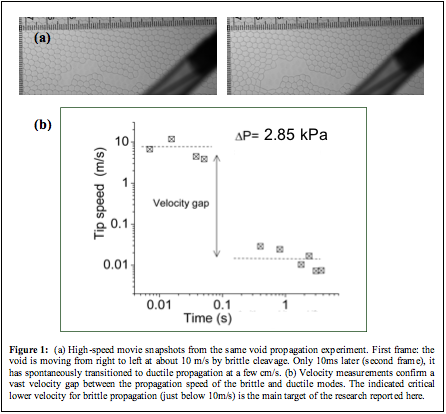
Transitions occurred spontaneously in experiment, and always from brittle to ductile (Fig.1a). After affirming the existence of an upper critical (maximum) velocity for ductile cracks (Hilgenfeldt, S. Arif, and J.-C. Tsai, Phil. Trans. Roy. Soc. 2008) and confirming its value theoretically, we proceeded to investigate a complementary observation of ours: a lower critical (minimum) velocity for brittle crack propagation. We find a significant velocity gap between the ductile speeds (cm/s) and brittle speeds, see Fig.1b. The brittle crack speed depends on driving pressure Æp, but lowering Æp causes brittle cracks to cease abruptly at a minimum speed of just below 10m/s.

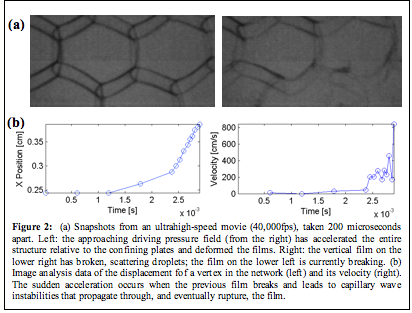
In this investigation, we used very high frame rates (up to 60,000 fps) to capture the rupture events of films associated with brittle failure (Fig.2a). The movies reveal that, as in ductile failure, local slip motion of vertices and Plateau border elements on the confining plates is crucial for the propagation of failure. In contrast to the ductile mode, where slip motion was balanced by capillary forces described by Bretherton's theory, here the slip motion accelerates, effecting film rupture and thus propagating the crack (Fig.2b, see also: S. Arif, Presentation at the 2008 APS Division of Fluid Dynamics meeting).

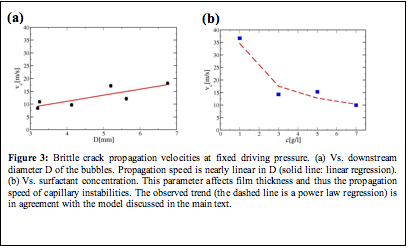
The time scale of breakage for each film is very consistent (given a fixed driving pressure), a finding backed by further experiments where we varied the bubble size and observed the brittle crack speed to scale with it (Fig.3a). The mechanism for film breakage appears to be the propagation of perturbations from the Plateau borders along the film (observed in the high-speed movies and consistent with typical capillary wave speeds). The latter means that thinner films should lead to larger velocities of brittle crack propagation, which we also verified experimentally (Fig.3b).

Even the thickest films only allow for propagation speeds down to a critical speed of about 10m/s (for our typical bubble size of 3mm). The explanation lies again in the Plateau borders sliding along the plate walls: If Æp is too small, viscous dissipation immediately balances the driving force and results in constant slip velocity - the propagation becomes ductile. If Æp is large enough, though, the sudden impact of the driving pressure on the leading bubble in the crack causes the Plateau borders to accelerate, exciting the capillary waves that break the films. We are developing a Navier-Stokes based model to predict critical driving pressures and critical velocities and compare with the obtained data (S. Arif and S. Hilgenfeldt. Critical velocities in foam fracture crack propagation, preprint, 2009).

As Æp increases, we find a rapid increase not only in crack speed, but in irregularity (roughness of the crack outline, see Fig.4).  We can investigate the details of this well-known phenomenon in crack propagation in traditional hard solids (particularly metals), as the scale of single "atoms" (bubbles) is accessible.  Irregularities are correlated with the position of frozen defects in the foam, typically those of 5-sided and 7-sided bubbles (penta/hepta defects). We are in the process of developing a model that adds the stress fields of such defects to the applied stress and indicates which films break in a given geometric configuration, and thus whether a crack roughening is expected.

Figure 1:  (a) High-speed movie snapshots from the same void propagation experiment. First frame: the void is moving from right to left at about 10 m/s by brittle cleavage. Only 10ms later (second frame), it has spontaneously transitioned to ductile propagation at a few cm/s. (b) Velocity measurements confirm a vast velocity gap between the propagation speed of the brittle and ductile modes. The indicated critical lower velocity for brittle propagation (just below 10m/s) is the main target of the research reported here.

Figure 2:  (a) Snapshots from an ultrahigh-speed movie (40,000fps), taken 200 microseconds apart. Left: the approaching driving pressure field (from the right) has accelerated the entire structure relative to the confining plates and deformed the films. Right: the vertical film on the lower right has broken, scattering droplets; the film on the lower left is currently breaking. (b) Image analysis data of the displacement fof a vertex in the network (left) and its velocity (right). The sudden acceleration occurs when the previous film breaks and leads to capillary wave instabilities that propagate through, and eventually rupture, the film.

Figure 3: Brittle crack propagation velocities at fixed driving pressure. (a) Vs. downstream diameter D of the bubbles. Propagation speed is nearly linear in D (solid line: linear regression). (b) Vs. surfactant concentration. This parameter affects film thickness and thus the propagation speed of capillary instabilities. The observed trend (the dashed line is a power law regression) is in agreement with the model discussed in the main text.

Figure 4:  (a) Foam with order map obtained by image analysis with MATLAB. Pentagons are indicated in red, heptagons in blue. (b) Superposition of initial defect structure and brittle crack path, demonstrating correlation between defect positions and deviations from straight propagation.