AmericanChemicalSociety.com

Granular media exhibit extraordinary properties due to their highly nonlinear and spatially discrete nature. In addition to their inherent theoretical interest, these materials are used or occur naturally in a wide array of settings. Our work is focused on pulse propagation in granular systems, a question that arises in varied circumstances ranging from underground detection to shock absorption.

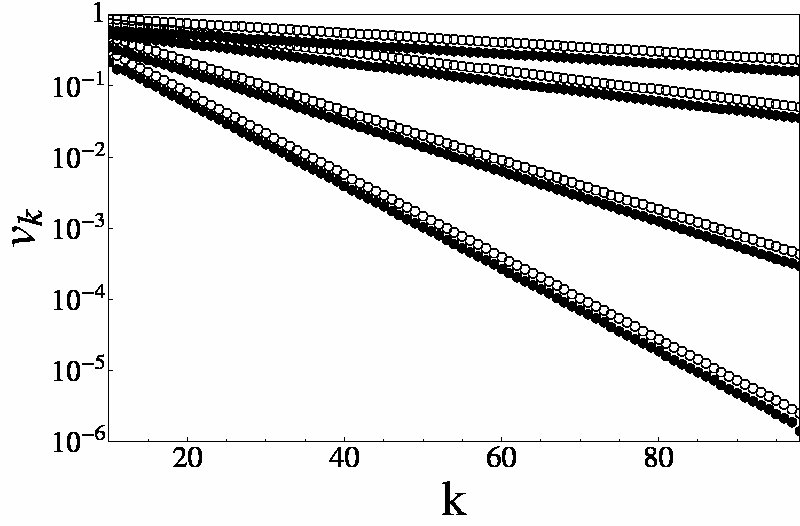
Pulse propagation in granular media has been studied primarily in granular chains. These simple physical constructs have served as a theoretical as well as experimental test bed for at least two decades. As simple as they may appear, the nonlinear interactions in this system had defeated analytical treatment and so everything that was known was based on specific experiments and numerical simulations. From these observations it was not possible to reliably extrapolate behavior to parameter ranges greatly different from those studied. Thus, for example, almost all experimental and numerical studies focused on chains of fewer than 20 granules, and could therefore say very little about much longer chains. In 2004 we began to construct an approximation that seemed to reproduce the characteristics of a propagating pulse along a chain to a remarkable degree of accuracy, . During this reporting period we have for the first time fully exploited this binary collision approximation (BCA), which relies on the simple notion that the propagation of a pulse involves only two granules at a time, thus reducing the many-body problem to a tractable two-body problem. The results have been nothing short of spectacular, with agreements between our theory and numerical simulations in the 1-2 percent range for a number of properties. We first applied this method to monodisperse chains as well as backward and forward tapered chains. Typical results can be seen in the adjacent figure. We show the decay of the velocity pulse amplitude for various tapering parameters in a backward tapered chain shown in the schematic. The differences between our analytic predictions and numerical simulations are barely discernible.

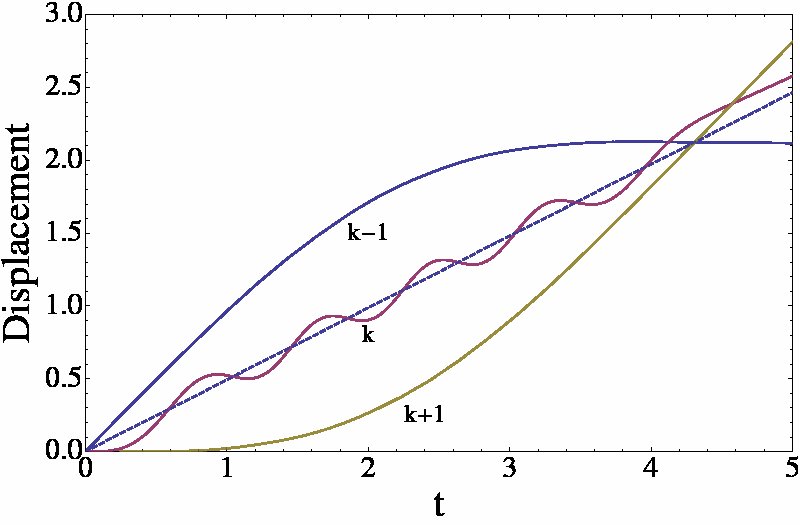
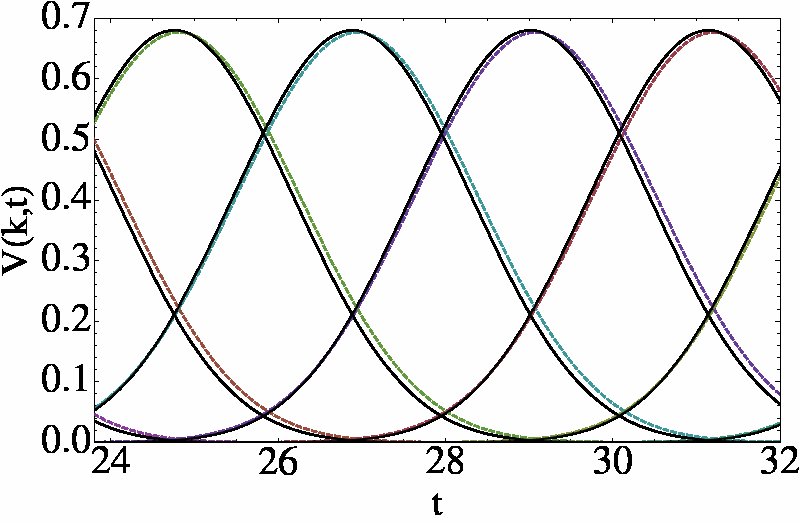
It has recently been argued that the pulse focusing or dispersion capability of a granular chain can be enhanced dramatically by decorating it with smaller granules placed between the bigger ones. A direct application of the BCA does not work here because the small granules oscillate back and forth several times as the pulse passes, as shown in the figure on the left. The interactions are no longer two-body. However, we have found a way to replace the decorated chain with an undecorated chain of effective masses and interactions. Again, the agreement between numerical simulations and theory is excellent, as seen in the typical results of the figure on the right, where we have superposed the analytical and numerical results. This major step opens the possibility to study more complex decorated chains that have been studied experimentally. Numerical simulations have recently indicated that an optimal design for pulse dispersion may be achieved through and optimization of the randomization of granular mass and size in such chains. This numerical work is severely limited in that only very short chains can be studied. We aim to extend our approach further to eventually be able to treat random chains using analytic methods.

We have only recently begun to work on pulse propagation in higher dimensional granular media, and this work is for now of necessity numerical. We have a fully functional computer code to simulate propagation in 2D dense granular systems. This is a highly nonlinear problem. Our code includes both translational and rotational degrees of freedom. We explicitly include the energy dissipation due to the viscoelastic nature of the medium. Another important property in 2D granular system is stretching between colliding granules, which occurs when their relative velocity is not along their axis of approach. Depending on the value of the friction coefficient, the colliding granules can stick together for a short time (stretching) or slip by each other. This surface friction is responsible for conversion of translational energy to rotational energy and vice versa. Our preliminary results indicate that when a single granule strikes a 2D hexagonal packed surface of identical granules, the energy imparted to the system propagates through it preserving the symmetry of the system. The amplitude of this pulse decays in time according to a power law, where the exponent in the decay law depends on the direction of pulse propagation.

During this period we also completed some work that was begun before this grant went into effect. We completed a study of heat conduction in one-dimensional granular gases, comparing the effects of different viscous dissipation mechanisms. One mechanism is momentum conserving, the other is not, and yet thermal conduction is normal in both cases. This belies an accepted notion of the role of momentum conservation in normal vs anomalous heat conductivity. We also completed a study of energy decay of a pulse propagating in a granular chain with damping proportional to the relative velocity of the grains. We observe a wave disturbance that at low viscosities consists of two parts exhibiting two entirely different time scales of dissipation. One is an attenuating solitary wave dominated by discreteness and nonlinearity, and has a the shorter lifetime. The other is a purely dissipative shoclike structure with a much longer lifetime and that exists only in the presence of dissipation.