From the pH of the ocean, the concentrations of the various carbonate species (H2CO3*, HCO3- and CO32-) can be determined. Since the concentration of hydronium ion is most easily measured as a pH value, it is more appropriate to describe equations 7 and 8 in terms of pH, rather than hydronium ion concentration. The pH of a solution is the negative logarithm of the hydronium ion concentration, so,
Thus, equations 7 and 8 can be rewritten:
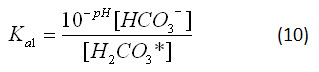
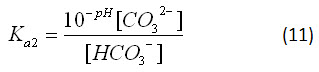
In an open solution, ions are free to dissolve into or evaporate out of solution. To determine the concentrations of these ions for the “Carbonates in an Open Ocean” graph in the applet, we can inspect the equilibrium constants for their reactions. Equation 4 shows that the concentration of carbonic acid (in all of its forms) is only dependent on the partial pressure of atmospheric carbon dioxide and the equilibrium constant for the reaction. Equation 4 can be rearranged:
In the applet, equation 12 was used to calculate the concentration of H2CO3, the logarithm of which was plotted in the open system graph. The atmospheric concentration of carbon dioxide, as set by the slider, is converted to a partial pressure and substituted into this equation. In the applet, KCO2=10-1.48 is used. This value was obtained by multiplying the K value for the dissolution of carbon dioxide into pure water (Henry's Law Constant: 3.36x10-4 mol L-1 kPa-1) by the atmospheric pressure (101.325 kPa) and dividing by the density of seawater, which accounts for the difference between pure and ocean water systems.7 The density value that is used is 1.025 kg/L, which is well within measured density ranges for seawater.8
Note that the graph displays the concentration of H2CO3*, which is the sum of the concentrations of carbonic acid and dissolved carbon dioxide. However, for simplicity's sake, this plot is labelled solely as carbonic acid. It is also interesting to note that the concentration of carbonic acid is independent of the pH and changes only with the concentration of atmospheric carbon dioxide.